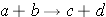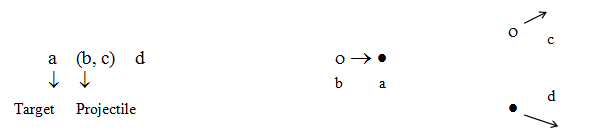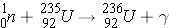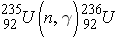ME754 Review I
Introduction to Nuclear Criticality Safety
REVIEW TOPICS PART I
This review covers the information you should have already been exposed to and hopefully remember. There are many opportunities to test your knowledge through the use of "Quiz Me" interactives. The answers appear whenever you click the Check Answer button. You will not be graded for this review, but you will receive 50 total points for completion of all five parts. This is essential foundational knowledge for this and following courses in the Nuclear Criticality Safety series.
ATOMIC AND NUCLEAR PHYSICS
Definitions
Let's begin with some definitions:
|
mass number
|
=
|
A, the total number of nucleons (neutron and proton) in a nucleus.
|
|
atomic number
|
=
|
Z, the number of protons in a nucleus.
|
|
nuclide
|
=
|

|
|
isotopes
|
=
|

|
|
isomers
|
=
|

|
|

|
=
|
symbol for nucleus of element X with atomic number Z and atomic mass number A.
|
|
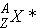
|
=
|
 in an excited state in an excited state
|
Fundamental Particles
The following particles are important in nuclear engineering (Lamarsh & Baratta, pp. 6-7).
Electron - Electrons can have a negative or a positive charge (these are rare). The electron has a charge of 1.60219×10-19 coulombs and a rest mass of 9.10954×10-31 kg.
Protron - Protons have a positive charge and rest mass of 1.67265 ×10-27 kg.
Neutron - Neutrons are electrically neutral and have a mass of 1.67495 ×10-27 kg.
Photon - Sometimes particles in nature don't always behave like particles but behave like waves. The photon is one of them and is associated with electromagnetic waves. Photons have both zero charge and rest mass and travels in vacuum at the speed of light (c=2.9979×108 m/sec).
Neutrino - The neutrinos, like the photons, have no electrical charge and zero rest mass
Particle Wavelengths
It was mentioned previously that particles have an associated wavelength. The wavelength l for particles that have zero rest mass (e.g., photons) is calculated from the expression [Id., equation 2.21]
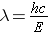
where . . .

The wavelength l for particles that have nonzero rest mass (e.g., neutrons) is calculated from the expression (Id., equation 2.16)
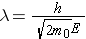
where . . .

It should also be mentioned that the kinetic energy of a particle of nonzero rest mass can be calculated from the expression (Id., equation 2.9)
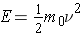
where . . .

while rest mass energy is calculated from the expression (Id., equation 2.4)
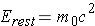
The total energy of photons (with a zero rest mass) is given by (Id., equation 2.13)
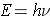
where . . .

RADIOACTIVE DECAY
Some nuclei are unstable and may spontaneously transform into a different nuclide while usually emitting energetic particles. This spontaneous nuclear transformation is called radioactive decay. The most common types of radioactive decay found in naturally occurring nuclides are:
Alpha decay
In alpha decay the nucleus emits a helium nucleus 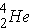 . The emission of an alpha-particle reduces Z by two and A by four. As an example, the alpha-decay of U-238 leads to [enter the correct element below] according to the equation (Id., p. 20)
. The emission of an alpha-particle reduces Z by two and A by four. As an example, the alpha-decay of U-238 leads to [enter the correct element below] according to the equation (Id., p. 20)


Beta decay
Beta decay corresponds to the conversion of a neutron in the nucleus into a proton, generally followed by the emission of an electron and a neutrino. The reverse can also take place for nuclei lacking in neutrons (i.e., the proton in the nucleus is transformed into a neutron followed by the emission of a positron and a neutrino) (Id., pp. 18-19). In beta-decay, . . .

Gamma decay
Gamma decay is the transition of a nucleus from one excited state to a lower excited state with the accompanying emission of a photon. The emitted photons have energies equal to the difference between the energies of the initial and final states, and are called gamma rays (Id., p. 18). Gamma decay . . .

The fundamental law describing radioactive decay states that the probability that a nucleus will decay in a given time interval is a constant independent of time. This constant is known as the radioactive decay constant, λ , and can be related to the number of original nuclei, N, left at time t through the following expression (Id., p. 23)
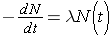
Note that λ has units of inverse time. Now, if initially N0 nuclei are present we can calculate the number of nuclei present at any later time t through the expression
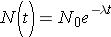
The rate at which nuclei are [_____] is given by the formula (Duderstadt & Hamilton 1976, p. 13)
Rate = 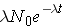

A related quantity is the radioactive half-life, T1/2, which is the length of time necessary for half of the original number of nuclei present to [_____}. The half-life can be calculated by noting
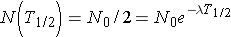
or (Id., equation 2.26)
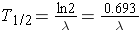

Another important quantity is that of the activity describing, or characterizing, a sample of radioactive material. The activity is the total number of disintegrations occurring per second λN(t) and is usually measured in units of curies (Ci) (Id., p.23). To derive an expression for the activity of a nuclide, we must first consider that most radioactive decay processes are a little bit more complicated than previously described. This is due to that the decaying nuclide may itself be produced by some source, R(t). The change in the number of original nuclide at a given time (or time interval) can then be expressed as
Time rate of change of the nuclide =
the rate of [_____] - the rate of [_____]loss

or symbolically
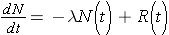
Integrating this equation and multiplying through by l gives the activity of the nuclide (Id., equation 2.30)
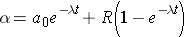
Another scenario that is often considered is the radioactive decay chain. Consider the decay chain
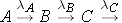
The number of nuclides of each type present can then be found through the expressions
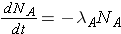
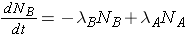
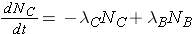
The integrated results of these equations are shown on p. 26 of the Lamarsh & Baratta. (equations 2.32 & 2.33).
As nuclear processes occur, the nuclides change in accordance with the illustration below (Chart of the Nuclides):
Instructions: Click each nuclide and drag it to its proper position on the chart above.
where . . .

STABLE NUCLIDES & BINDING ENERGY
Nuclear forces acting among nucleons (neutrons & protons) in a stable nucleus are such that the ratio of A to Z increases with Z. This means that stable nuclides become [_____] neutron-rich with [_____] Z. This is illustrated below in the nuclear stability curve (Stacey 2001, Figure 1.1).

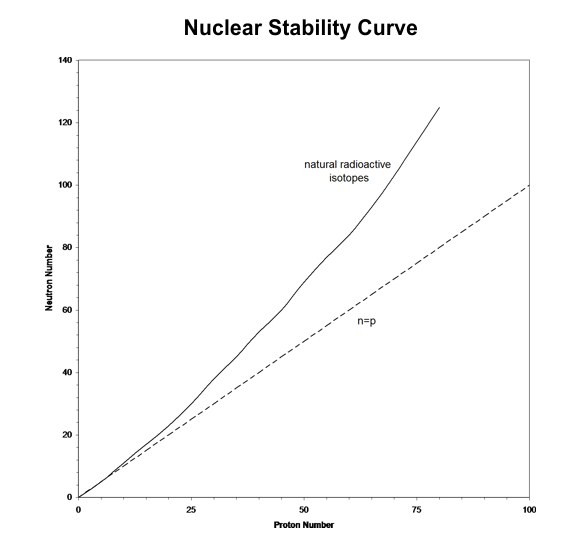
Because the actual mass of an atomic nucleus is not the sum, the stable nuclides have a mass defect. The mass defect is defined as (Id., equation 2.43)
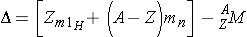
where,

∆, when expressed in energy units, is equal to the energy that it takes to break the nucleus into its constituent nucleons.
Summary
Binding energy of the nucleus = The amount of [_____] supplied energy that would be converted to mass in disassembling a nucleus into its separate nucleons.

The splitting of very high A nuclides to form intermediate-A nuclides with a higher binding energy per A value is the basis of the [_____] process for the release of nuclear energy, while the combination of low A nuclides to form higher A nuclides with a higher binding energy per A value is the basis of the [_____] process (Stacey 2001, pp. 3-4). The binding energy per nucleon as a function of Z is illustrated in Figure 2.8 of Lamarsh & Baratta.

The binding energy is also known as the [_____] energy. The separation energy, ES, of the last neutron (this is the least bound) can be calculated from the expression (Id., equation 2.45)

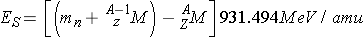
The separation energy is enough to [_____] a neutron [_____] the nucleus but it does not provide any kinetic energy to the nucleus.

It should also be mentioned that there are some "magic" nuclei with nucleons know as "magic numbers". The "magic numbers" (neutrons or protons) are: hint - consult the periodic table.


As an example, 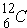 is a weak absorber because of "magic number". Further,
is a weak absorber because of "magic number". Further, 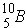 is a strong absorber because it has 1 less neutron than the "magic number". Also, when there are an odd number of neutrons, the last neutron is weakly bound.
is a strong absorber because it has 1 less neutron than the "magic number". Also, when there are an odd number of neutrons, the last neutron is weakly bound.
NUCLEAR REACTIONS
Nuclear reactions are taking place when two nuclear particles interact to produce two or more nuclear particles or gamma rays. The following notation is frequently used to describe nuclear reactions (Id., equation 2.34):
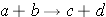
Sometimes a more detailed notation is used since one particle is generally considered to be a projectile while the other particle is taken as a target (Duderstadt & Hamilton 1976, p. 15):
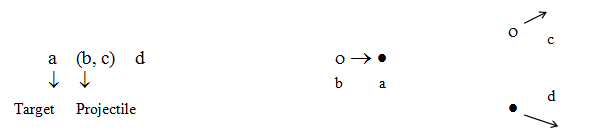
As an example, the reaction
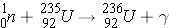
would be written as
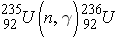
For the reaction a(b,c)d, the reaction energy (or Q-value) is calculated as (Id., equation 2.37):
Q = ((Ma + Mb) - (Mc + Md)) c2
where . . .
M = atomic mass of the nuclide
c = speed of light (converted into energy in a reaction)
Q is expressed in MeV. Recalling that 1 amu is 931.494 MeV, the Q value can be written as
Q = ((Ma + Mb) - (Mc + Md)) 931.494 MeV



Proceed to Part II




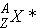
 in an excited state
in an excited state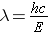

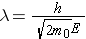
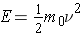
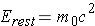
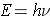
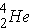 . The emission of an alpha-particle reduces Z by two and A by four. As an example, the alpha-decay of U-238 leads to [enter the correct element below] according to the equation (Id., p. 20)
. The emission of an alpha-particle reduces Z by two and A by four. As an example, the alpha-decay of U-238 leads to [enter the correct element below] according to the equation (Id., p. 20)

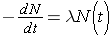
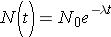
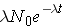
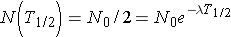
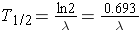
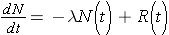
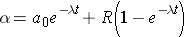
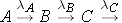
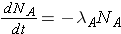
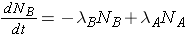
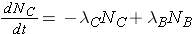

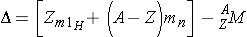
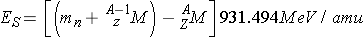
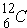 is a weak absorber because of "magic number". Further,
is a weak absorber because of "magic number". Further, 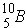 is a strong absorber because it has 1 less neutron than the "magic number". Also, when there are an odd number of neutrons, the last neutron is weakly bound.
is a strong absorber because it has 1 less neutron than the "magic number". Also, when there are an odd number of neutrons, the last neutron is weakly bound.