ME754 Review Topics III
Continuing . . .
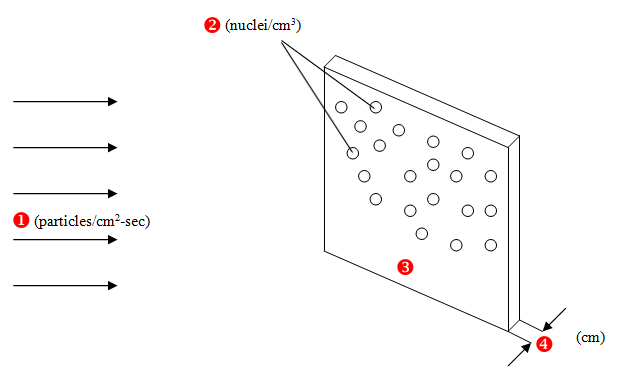
Microscopic cross sections describe the likelihood that a neutron will interact with a given nucleus. Consider a beam of neutrons, all with the same velocity, normally (perpendicularly) incident on a very thin plate of some material as illustrated in the figure below. Assume that the target is so thin that all nuclei "see' the same beam intensity. (This is a limiting case - we can only approach this "thin limit" with very thin targets.)
The rate at which neutrons collide with nuclei must be proportional to IA (the rate at which neutron strike) and to N D x (the areal density of target nuclei). Putting this statement into mathematical language, and using the symbol s to represent the constant of proportionality, we get the following:
Rate = δΙΑΝ∆x, or
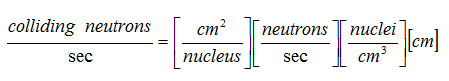
We have determined that s must have units of area (or to be exact, area per nucleus). The symbol s is referred to as a "microscopic cross section" and is tabulated in units of barns (1 barn = 10-24 cm2). It might be useful to think of σ as the effective area that a nucleus presents to a neutron.
Earlier we described s as a "constant" of proportionality. However, if we changed anything about our simple experiment, we might expect our "constant" to change. That is, we might expect to have a different σ for different neutron speeds and for different target nuclei. In fact, microscopic cross sections depend on:
In the preceding discussion we were looking at the total rate at which neutrons interact with nuclei, without distinguishing between kinds of interactions (elastic scattering, fission, inelastic scattering, capture, etc.). The σ that we used above is called the microscopic total cross section, and is denoted σt. It can be thought of as the sum of microscopic cross sections for various specific interactions:
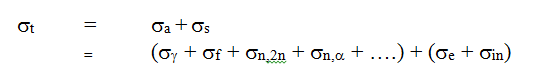
where . . .
We can also assign separate cross sections to characterize elastic scattering σe in which the target nucleus remains in its ground state, and inelastic scattering σin in which the target nucleus is left in an excited state. The scattering cross section is therefore the sum of the elastic and inelastic scattering cross section (Id., p. 55; Duderstadt & Hamilton 1976, p. 18):
σs = σe + σin
Note that cross sections are related to probabilities of various types of reactions.
Based on the previous discussion, the neutron cross section hierarchy is illustrated below. Match the circled numbers (1-9) with the correct labels.
NOTE: Some answers below are interchangeable. However, machine scoring cannot account for this. If your answers appear incorrect, you can reverse your answer or simply ignore the score. (You get to report your better score when you submit your review credit.)
We have seen that quantitative descriptions of neutron-nuclear interactions involve microscopic cross sections. The microscopic cross sections are almost always multiplies by the number density (nuclei/cm 3 ) of the target nuclei. It is therefore convenient to define the macroscopic cross section as the product:
x = macroscopic "x" cross section
= Number Density x Microscopic Cross Section (cm-1)
of each different type, x = {t, a, s, g , f, .....}, of interaction. Note that macroscopic cross sections have unit of inverse length:
(nuclei/cm3) · (cm2/nucleus)=cm-1.
In addition, macroscopic cross sections have an important physical interpretation. The macroscopic cross section for any type of reaction is the expected number of reactions (of that type) per unit neutron path length. Another way of saying this is that the macroscopic cross section is the probability per unit path length that a neutron will interact.
To illustrate, recall the equation below for the reaction rate:
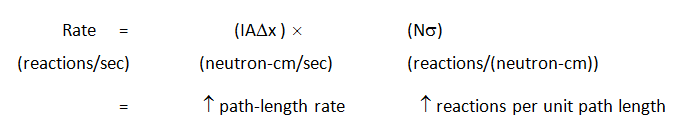
The term "macroscopic" comes from the recognition that St characterizes the probability of neutron interaction in a macroscopic chunk of material (the target), whereas the microscopic cross section characterizes the probability of interaction with only a single nucleus.
Let's return to our uniform beam of mono-energetic neutrons incident normally upon a slab target. This time we allow the target to be thick as shown in the figure below.
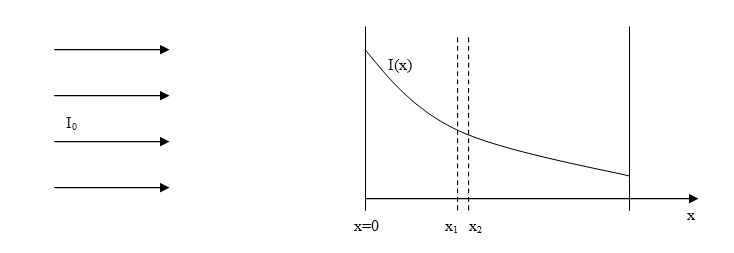
Let's define:
I(x) = intensity of uncollided neutrons at distance x into the target (neutrons/cm2 - sec)
= intensity of neutrons that have reached distance x without interacting with any nuclei.
The conservation equation states:
The conservation equation is used to find:
(A) = (B) + (C) - (D)
Create the correct equation by matching the correct term with each letter designation (A-D):
There is no mechanism for adding to the uncollided intensity, so the second term on the right-hand side is zero. Assuming that (x2-x1) is very small (so that this is a "thin" slice of the target), the intensity removed can then be given by the equation Rate = σIAN∆x divided through by the area "A". The conservation statement, written mathematically, is therefore:
Upon rearranging and recognizing the macroscopic cross section, we find:
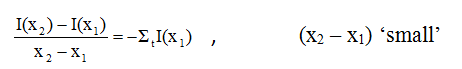
Taking the limit as x2 approaches x1 (so the slice really is thin), we obtain a differential equation:
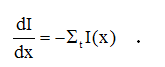
This equation, which describes the attenuation of a beam, is of exactly the same form as the equation that describes radioactive decay (dN/dt = R(t) -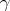 
N(t)), and its solution is (Lamarsh & Baratta, equation 3.11):
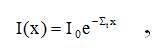
where I0 is the uncollided intensity at x=0. Thus, uncollided neutrons are exponentially attenuated as they try to pass through matter.