ME754 Review Topics IV
Continuing . . .
The average distance that a neutron travels without interacting is known as the mean free path. We can define a probability density ( ≈ distribution) function for first collision in our beam problem:
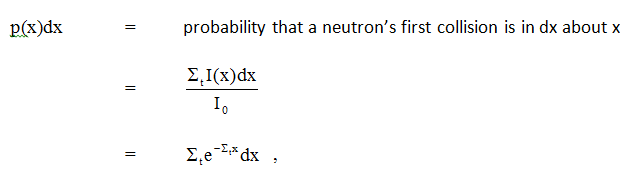
which means the probability density function (pdf) for first collision is p(x) = 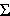 te-
te-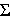 t x. We can use this pdf to obtain averages. For example:
t x. We can use this pdf to obtain averages. For example:
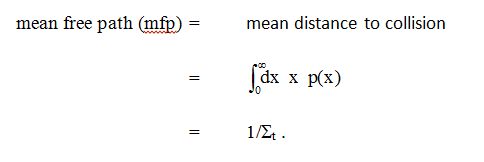
The mean free path is the reciprocal of the macroscopic cross section. It follows from their definitions that macroscopic cross sections are additive in the same way that microscopic cross sections are:
Match the numbers within the hierarchy with the proper terms: Σt Σs Σa Σin Σe Σs Σn,2n Σn,α Σ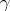
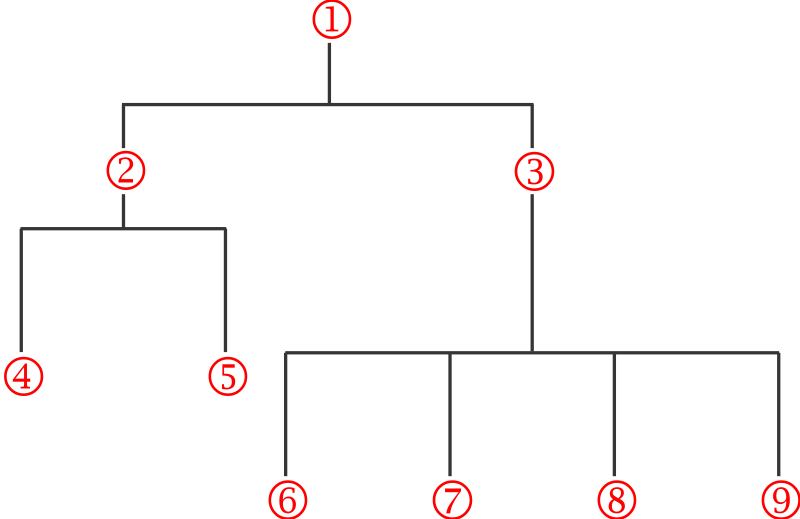

In addition, given:
a mixture of nuclides: YA, YB, ....,
with number densities: NA, NB, ....,
and microscopic cross sections: σx A, σx B, .....,
then for any type, x, of interaction, the macroscopic cross section for the mixture is:
The neutron flux, f , may be defined as the total number of neutrons that passes through a unit area normal to their direction per second. In the event all neutrons have the same speed v and have a neutron density of n neutrons per unit volume, then the flux can be defined as (Lamarsh & Baratta, equation 3.20):
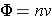
The units of neutron flux are neutrons/cm 2 - sec (same units as the beam intensity). The interaction rate per unit volume (or the collision density) can be described in terms of the flux as (Lamarsh & Baratta, p. 61):

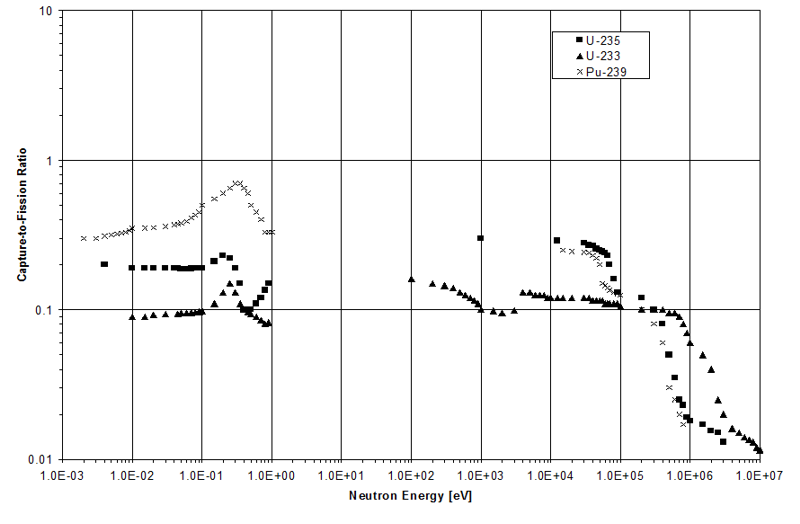
When a neutron is absorbed by a fissile isotope such as 235U, it may cause that isotope to fission. It is also possible that the compound nucleus formed by the neutron absorption, 236U*, may instead decay to its ground state by gamma emission. This relative balance between the probability of fission and radiative capture is referred to as capture-to-fission ratio and is defined by (Lamarsh & Baratta, equation 3.45):

This ratio depends on the isotope of interest and the incident neutron energy E. The capture-to-fission ratio is plotted in the figure below (adapted from Duderstadt & Hamilton 1976, Figure 2-19) as a function of neutron energy for three of the primary fissile nuclides. It can be seen from the figure that most neutron absorption in these isotopes leads to fission events.
Let's begin with a definition:
η = expected (or average) number of neutrons produced per neutron absorbed in fuel (i.e., a fissile nucleus)
For a fuel composed of a single fissile isotope , we can write:
η =  σf / σa =
σf / σa =  /(1+ α)
/(1+ α)
where 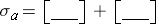
Select the correct order of terms:

Most fuels, however, contain a mixture of isotopes. In this case, the macroscopic fission and absorption cross sections will be utilized the following way to characterize each isotope:
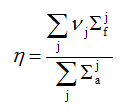
Note that h (E) is generally of the order of 2 for low-energy neutrons, but increases with energy above 0.1 MeV as the capture-to-fission ratio falls off (see previous figure illustrating the capture-to-fission ratio as a function of neutron energy).