(Duderstadt & Hamilton 1976, p. 24):ME754 Review Topics V
Continuing . . .
Cross sections for neutron interactions are in many cases not constant, but vary with neutron energy. In the low energy region of most nuclei, the capture cross section varies at 1/√E, or as 1/v since the neutron speed v is proportional to √E (E is the neutron energy). The 1/v region is illustrated in Figure 3.5 of Lamarsh & Baratta (p. 65). In the same figure, a sharp peak, or resonance, is shown in the intermediate energy range. This characteristic of cross sections can be explained by considering a neutron incident upon a nuclide 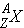(Duderstadt & Hamilton 1976, p. 24):
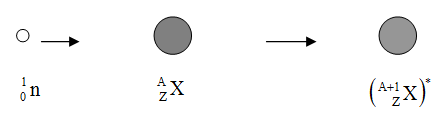
The energy available for such reaction in the center of mass (CM) energy is:
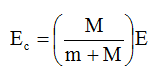
where . . .
The actual energy of the excited level of the compound nucleus is much higher due to the additional binding energy of the added neutron Eb. If Ec + Eb is very close to a nuclear energy level of the compound nucleus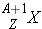 
, it can be expected that the probability for compound nucleus formation will be much larger than if Ec + Eb does not "match" this energy level. Therefore, we expect that the cross sections for such compound nuclear reactions will exhibit sharp peaks, or resonances, at those neutron energies E for which this energy matching occurs.
Resonances occur in cross sections because nuclei can be very hungry for neutrons of certain energies, and at the same time can find other neutrons quite distasteful. This is understandable in terms of the energy levels of a nucleus illustrated below (adapted from Bennet & Thomson 1988, Figure 2.11).
Match the numbers in the chart with the correct description.
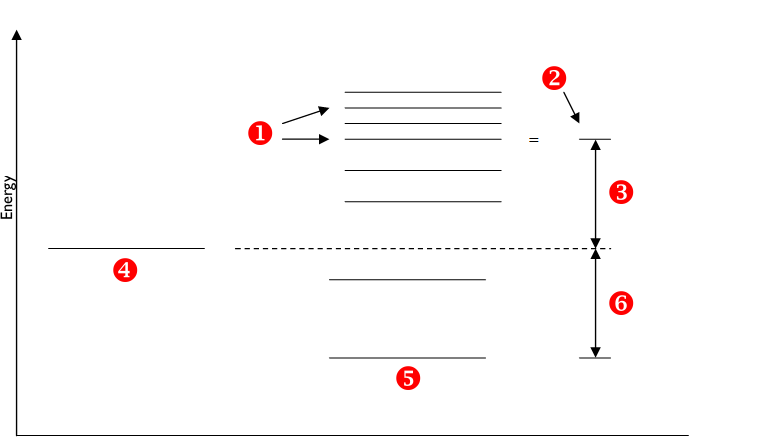
Energy Levels and Resonance Absorption
If the energy of the neutron is such as to produce the compound nucleus at or very near one of its excited states, as shown in the figure above, the probability of the interaction taking place is very high. This corresponds to a high value of the cross section. If, on the other hand, the energy of the incident neuron is such as to produce the compound nucleus at some energy midway between two excited levels, the probability of the interaction is very low. This corresponds to a low value of the cross section.
In Summary:
When the energy is just right, the cross section will be high. Otherwise, it will be much lower. The high part is called a (select the correct combination below):
The cross section for any reaction involving a compound nucleus will exhibit resonances. The only reaction that does not involve a compound nucleus is [_____] scattering, in which the neutron scatters off of the nucleus without ever penetrating it (as previously stated). Select the correct term below.
Under reasonable assumptions, it is possible to derive a formula for s around a resonance. For example, the Breit-Wigner formula (Lamarsh & Baratta, equation 3.23) gives σ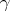
as a function of E, for E at and near a single-level resonance. Characteristics of nuclei of different mass numbers are summarized in the figure below (adopted from Figure 2-1 in Duderstadt & Hamilton 1976).
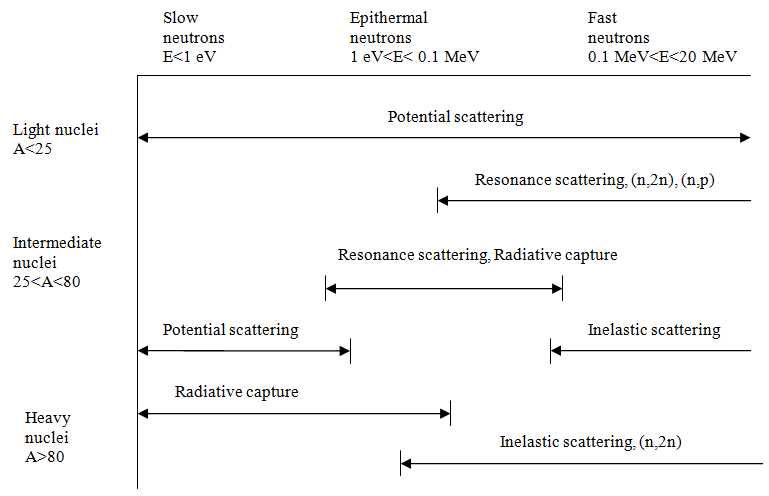
Based on the figure above, the following general trends can be stated about the following reactions (select the correct values for each type of reaction):
Exceptions to these trends exist for the "magic" nuclei with nucleons known as "magic numbers" (these were discussed previously).
As mentioned earlier, neutrons are produced by fission at an average energy of about [___] MeV (indicate the correct value below). Further, we know that [_____] energy neutrons are the most effective for causing fission, demonstrated in the table below (Stacey 2001, Table 1.3), as the value for σt rises at [_____] energy.
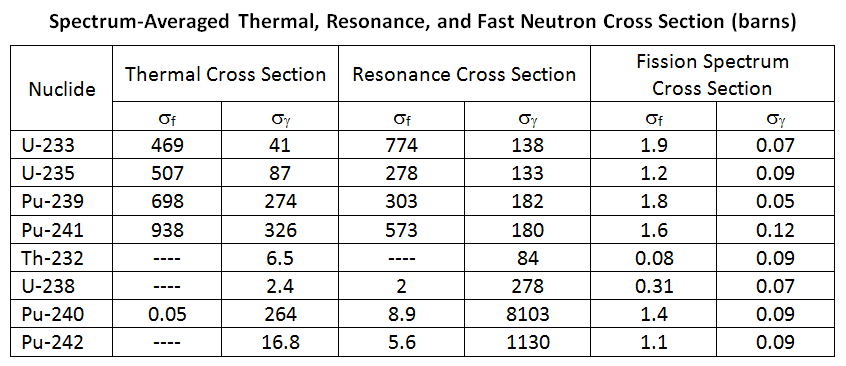
Since neutrons are produced by fission at [_____] energy and are most effective in causing fission at [_____] energy, an important process in a reactor is the [___ ___] of neutrons. This can be accomplished through scattering collisions where the energy of the neutron is progressively reduced. The process to slow down fast neutrons is known as [_____]. Select the correct terms below.
One of the most basic things we must be able to do is to predict whether the reactor power will increase, decrease, or stay the same. We choose to characterize this using the reactor's multiplication factor.
We are interested in maintaining a fission chain reaction. As discussed earlier, when a neutron causes a fission, the result is:
Select the correct values below.
Each neutron in this "new generation" either escapes the reactor or gets absorbed in it. If absorbed, a neutron may cause another fission, keeping the process going. We define (Lamarsh & Baratta, equation 4.1):
Then:
Correctly match the terms below.
Note that keff is a property of the system under study, not of the neutrons in the system.
Another definition of the multiplication factor is:
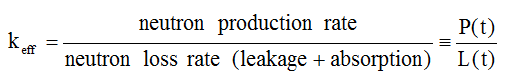
It is necessary to balance the rate at which neutrons are produced with the rate at which they disappear in order to make a reactor critical. Neutrons can disappear, as mentioned earlier, in two ways:
Therefore,
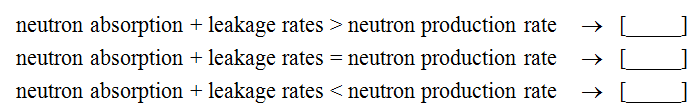
Select the correct order of terms:
The production, absorption, and leakage rates depend on the size/geometry and composition of the reactor/system. We will discuss this topic further later in the course.
We shall develop here a formula for the multiplication factor keff in a thermal reactor. We do so by considering the life history of a neutron from birth to death, and describing each fork in the road via a mathematical statement of probability. First, we define:
We now sketch a neutron's history in a thermal reactor. You will need to identify what physical process takes place provided that the neutron does not leak out of the system. Drag the symbols on the left to their proper place on the graph. You will receive immediate feedback.
It follows that the multiplication factor must be:
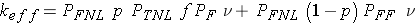
It is customary to define
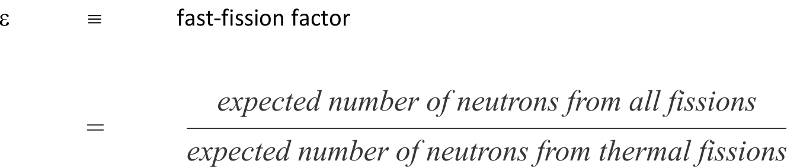
This gives us the six-factor formula:
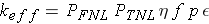
In an infinite medium nothing leaks, and we have the four-factor formula for the infinite-medium multiplication factor,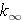 
:
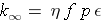
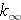is an upper bound for Keff
The six- and four-factor formulas provide insight into how a system's physical characteristics affect the multiplication factor.
REFERENCES
D.J. Bennet & J.R. Thomson, The Elements of Nuclear Power, John Wiley & Sons (1988).
J.J. Duderstadt & L.J. Hamilton, Nuclear Reactor Analysis, John Wiley & Sons (1976).
J.R. Lamarsh & A.J. Baratta, Induction to Nuclear Engineering, Prentice Hall (2001).
W.M. Stacey, Nuclear Reactor Physics, John Wiley & Sons (2001).
Parrington, J.R.; Knox, H.D.; Breneman, S.L.; Baum, E.M.; and Feiner, F. 1996. Nuclides and Isotopes, Chart of the Nuclides. 15th Edition. San Jose, California : General Electric Company and KAPL, Inc.