Circuit states

Let's talk in terms of "on" or "off". In an electrical circuit, when a voltage is present we say that the circuit is "on". When there is no voltage present, we say that the circuit is "off".

We represent these states with the digits 0 and 1:

• the "zero" state means the circuit is off -> 0
• the "one" state means the circuit is on -> 1

Consider the three diagrams shown below, the binary logic ciruit, the AND gate and the OR gate. Each of these example circuits have the following components:

• a power source (such as a battery)
• a switch (or switches)
• a light bulb

These circuit components are represented by the following symbols, and in the case of the switch, the logic state that it can represent.

Component	Component Description	Logic State
	Wire, an electrical conductor that transmits signals	0
	Switch is shown open (the switch is off)	0
	Switch is shown closed (the switch is on)	1
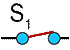	Switch is shown closed (the switch is on) and is labeled "S1". Labeling is common in circuits where there is more than one of a type of component in a circuit.	1
	Lightbulb	n/a
	Battery (the power soure)	n/a

 

In the circuits below the switches are initially open, in the off position, and the circuit is known to be in the 0 state. When the switch(es) are turned on in the proper configuration, the circuit is in the 1 state and the light bulb illuminates.

And now, a description of each of the circuits.

Note: In the following diagrams, click on the switches to see how they affect the circuit.

Binary logic

We can represent the position of the switch in a circuit, along with the corresponding states, in a "truth table":

When the switch is closed, the lightbulb illuminates and the circuit is in the "on" or the "1" state.

 

AND logic

Now consider two switches connected in series (i.e., one right after another in the circuit). We now have two switch positions that influence the light status:

When S1 AND S2 are closed, the lightbulb illuminates and the circuit is in the "on" or the "1" state.

 

We call this combination of switch positions AND logic:

• 0 AND 0 yield a 0 result
• 0 AND 1 yield a 0 result
• 1 AND 0 yield a 0 result
• 1 AND 1 yield a 1 result

OR logic

Now consider two switches again, but this time in parallel (i.e., connected on separate branches from the "main" circuit). We still have two switch positions to consider in determining the light status, but the outcomes behave in a different way:

When S1 OR S2 is closed, the lightbulb illuminates and the circuit is in the "on" or the "1" state.

We call this combination of switch positions OR logic:

• 0 AND 0 yield a 0 result
• 0 AND 1 yield a 1 result
• 1 AND 0 yield a 1 result
• 1 AND 1 yield a 1 result

We call these diagrams truth tables, and they form the basis for what is known as Boolean logic. Boolean logic contains the basic principles of digital operation that allow the CPU to operate in a coordinated manner to achieve the desired result.