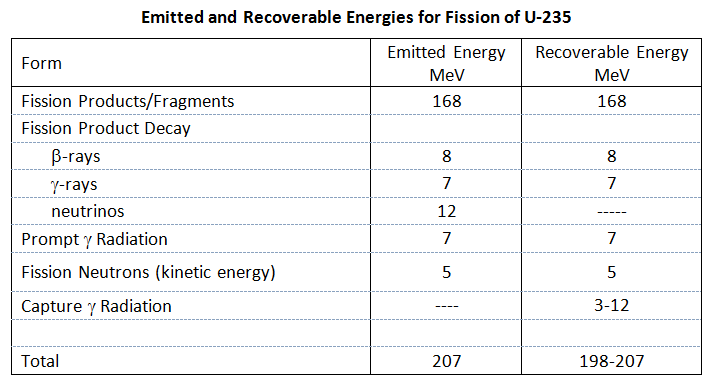
Compound Nucleus Formation

The basis for compound nucleus formation is that incident neutron gets absorbed into the original nucleus to form a compound nucleus in the following manner:

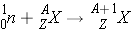
As stated earlier, compound nucleus formation includes the processes for the neutron being captured in the nucleus, being scattered, or causing the fission of the nucleus. These processes are described below.

Radiative Capture

Radiative Capture (n, g ) occurs the following way:

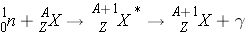
In radiative capture, a neutron appears/disappears and the excited nucleus decays immediately and emits [_____] radiation. An example of this reaction is:

 

Value: 3

238U + 1n [___] [___] + [___]

 
 
 
 

Inelastic Scattering

Inelastic Scattering (n,n ¢ ) occurs the following way:

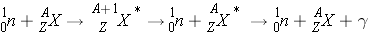
 Inelastic scattering alters both the kinetic energy and the internal energy of the nucleus, leaving it excited for a moment before it expels its excess energy in the form of one or more gammas.   Unlike elastic scattering, inelastic scattering does not conserve energy since some of the original kinetic energy is transformed to gamma radiation and the total kinetic energy is less than it was before the reaction.   Neutrons lose on average much more energy per collision in inelastic scattering events than in the case of elastic scattering events with the same nucleus.

Fission

A brief description of the theory of fission can be achieved through the liquid drop model.   The sort range nuclear forces, which are analogous to the surface tension of a liquid drop, hold the nucleus in a more or less spherical shape in the same way that a liquid drop is spherical.   However, if the nucleus is excited, possibly as a result of absorbing a neutron, its shape may be distorted.   It is possible that this distortion may lead to a dumbbell shape at which point the Coulomb force of repulsion between the two halves of the dumbbell exceeds the nuclear force (holding the nucleus together) which is weakened by the distortion of the nucleus.   Once this point is reached the nucleus splits into two fragments.

 

Value: 1

Fission of U-235, illustrated below, first includes the [_____] of a neutron to form U-236 in an excited state.

 
 

 

Value: 1

U-236 then splits into [_____] fission fragments whose mass numbers vary between about 70 to 160 (see fission product spectrum for thermal fission neutrons in Lamarsh & Baratta, Figure 3.12) and a few neutrons along with gamma radiation, neutrinos and energy is also being released. 

 
 
 

Fission (n,f) can be described as:

FissionProcess.png

 

The exact identity of the fission products and the number of neutrons vary between fissions. The following reaction is, however, typical:

In this example the fission products (i.e., La-147 and Br-87) are not the same, which is more likely to occur than fission with two products of equal mass.  The most probable mass numbers to occur are between 96 and 135 as shown by the fission yield curve in Lamarsh & Baratta (p. 82, Figure 3.12).

The number of neutrons emitted per fission varies from one event to another, and also depends on the isotope undergoing fission as well as the energy of the incident neutrons.  In addition to U-235, the following nuclides are also fissile (select all that apply):

[mark all correct answers]

 
 
 
 
 
 
 

 

There are also fissionable nuclides that are susceptible to fast neutron fission. They are:

[mark all correct answers]

 
 
 
 
 
 
 

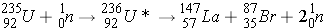
The table below shows the average number of neutrons emitted per fission for various isotopes (Id., Table 3.4; Bennet & Thomson 1988, Table 2.1) .   The parameter for the average number of neutrons emitted per fission is denoted ν.

NeutronsEmittedPerFission.png

It can be seen from the table above that n depends on the fissioning nuclide and on the energy of the neutron causing fission.   The equations to calculate the average number of neutron emitted per fission for U-235, U-233, and Pu-239 as a function of incident neutron energy are as follows (Stacey 2001, Figure 1.10):

Vu-235.png

E is in units of MeV.

Based on the fission energy spectrum (Id., Figure 3.14) and the equation describing the spectrum (Id., equation 3.56), it can be noted that the average energy of fission neutrons is approximately 2 MeV.

The energy release in fission is around 200 MeV.   Now, there is a difference between the energy being released in the fission process and the energy that can be recovered in a reactor (to produce heat).   The table below distinguishes between the emitted and recoverable energy for the fission of U-235 (Id., Table 3.6). It can be seen that the kinetic energy of the fission products/fragments accounts for the majority of the energy release. Note that the 5 MeV of kinetic energy of neutrons is estimated based on an average of 2.5 neutrons per fission with an average kinetic energy of 2 MeV each.

EmittedRecoverableEnergiesForFissionU-235.png

 

Proceed to Part III


return to top | previous page