THE MULTIPLICATION FACTOR, keff

 One of the most basic things we must be able to do is to predict whether the reactor power will increase, decrease, or stay the same.   We choose to characterize this using the reactor's multiplication factor.

 We are interested in maintaining a fission chain reaction.   As discussed earlier, when a neutron causes a fission, the result is:

Select the correct values below.

 

Value: 2

  • new, [_____] nuclides ([_____] products). Select the correct combination below.

 
 
 
 

 

Value: 1

  • about [___] MeV of energy (converted from matter).

 
 
 

 

Value: 1

  • a few more neutrons ([___])

 
 
 

Each neutron in this "new generation" either escapes the reactor or gets absorbed in it.   If absorbed, a neutron may cause another fission, keeping the process going.   We define (Lamarsh & Baratta, equation 4.1):

MultiplicationFactor.png

Then:

NeutronPop.png

Correctly match the terms below.

 

Value: 3

Match the items.

The task is to match the lettered items with the correct numbered items. Appearing below is a list of lettered items. Following that is a list of numbered items. Each numbered item is followed by a drop-down. Select the letter in the drop down that best matches the numbered item with the lettered alternatives.

a. subcritical

b. critical

c. supercritical

 

Note that keff is a property of the system under study, not of the neutrons in the system. 

Another definition of the multiplication factor is:

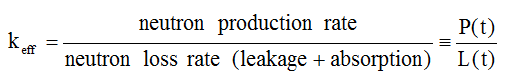
MultiplicationFactorKeff.png

It is necessary to balance the rate at which neutrons are produced with the rate at which they disappear in order to make a reactor critical.   Neutrons can disappear, as mentioned earlier, in two ways:

Therefore,

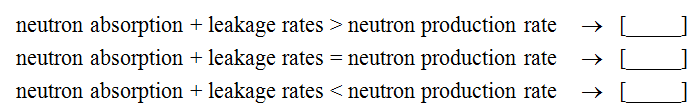
NeutronProductionRate.png

Select the correct order of terms:

 

Value: 3

Select the correct order of terms to complete the above.

 
 
 
 

The production, absorption, and leakage rates depend on the size/geometry and composition of the reactor/system.   We will discuss this topic further later in the course.

 


return to top | previous page | next page