MACROSCOPIC CROSS SECTIONS

We have seen that quantitative descriptions of neutron-nuclear interactions involve microscopic cross sections.   The microscopic cross sections are almost always multiplies by the number density (nuclei/cm 3 ) of the target nuclei.   It is therefore convenient to define the macroscopic cross section as the product:

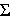x      =   macroscopic "x" cross section

          =   Number Density x Microscopic Cross Section (cm-1)

 

of each different type, x = {t, a, s, g , f, .....}, of interaction.   Note that macroscopic cross sections have unit of inverse length:

(nuclei/cm3) · (cm2/nucleus)=cm-1.

In addition, macroscopic cross sections have an important physical interpretation.   The macroscopic cross section for any type of reaction is the expected number of reactions (of that type) per unit neutron path length. Another way of saying this is that the macroscopic cross section is the probability per unit path length that a neutron will interact.

To illustrate, recall the equation below for the reaction rate:

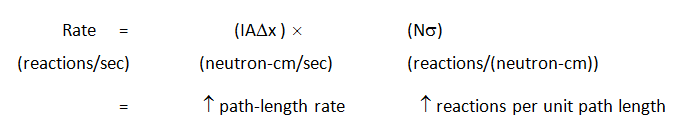
ReactionRateFormula.png

The term "macroscopic" comes from the recognition that St characterizes the probability of neutron interaction in a macroscopic chunk of material (the target), whereas the microscopic cross section characterizes the probability of interaction with only a single nucleus.

ATTENUATION

Let's return to our uniform beam of mono-energetic neutrons incident normally upon a slab target.   This time we allow the target to be thick as shown in the figure below.

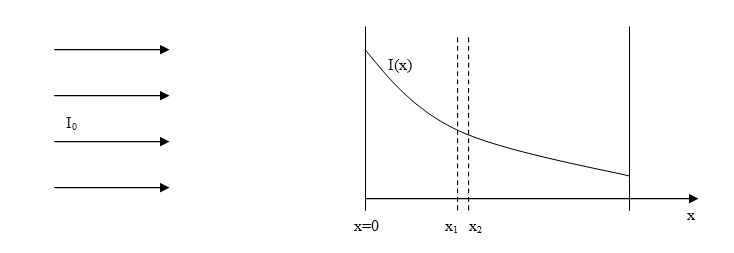
Attenuation.png

Let's define:

I(x)   =    intensity of uncollided neutrons at distance x into the target (neutrons/cm2 - sec)

         =    intensity of neutrons that have reached distance x without interacting with any nuclei.

The conservation equation states:

ConservationEquation.png

The conservation equation is used to find:

(A) = (B) + (C) - (D)

Create the correct equation by matching the correct term with each letter designation (A-D):

 

Value: 1

Match the items.

The task is to match the lettered items with the correct numbered items. Appearing below is a list of lettered items. Following that is a list of numbered items. Each numbered item is followed by a drop-down. Select the letter in the drop down that best matches the numbered item with the lettered alternatives.

a. Intensity at X2

b. Intensity added between X1 and X2

c. Intensity removed between X1 and X2

d. Intensity at X1

 

There is no mechanism for adding to the uncollided intensity, so the second term on the right-hand side is zero.   Assuming that (x2-x1) is very small (so that this is a "thin" slice of the target), the intensity removed can then be given by the equation Rate = σIAN∆x divided through by the area "A".   The conservation statement, written mathematically, is therefore:

ConservationStatement.png

Upon rearranging and recognizing the macroscopic cross section, we find:

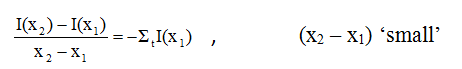
MacroscopicCrossSection.png

Taking the limit as x2 approaches x1 (so the slice really is thin), we obtain a differential equation:

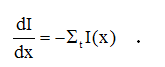
DifferentialEquation.png

This equation, which describes the attenuation of a beam, is of exactly the same form as the equation that describes radioactive decay (dN/dt = R(t) - N(t)), and its solution is (Lamarsh & Baratta, equation 3.11):

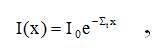
AttenuationBeam.png

where I0 is the uncollided intensity at x=0.   Thus, uncollided neutrons are exponentially attenuated as they try to pass through matter.

 

Continue to Part IV

After finishing this lesson, complete the form below:

Type your name or identifier:


return to top | previous page