RADIOACTIVE DECAY
Some nuclei are unstable and may spontaneously transform into a different nuclide while usually emitting energetic particles. This spontaneous nuclear transformation is called radioactive decay. The most common types of radioactive decay found in naturally occurring nuclides are:
Alpha decay
In alpha decay the nucleus emits a helium nucleus 
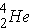. The emission of an alpha-particle reduces Z by two and A by four. As an example, the alpha-decay of U-238 leads to [enter the correct element below] according to the equation (Id., p. 20)
Beta decay
Beta decay corresponds to the conversion of a neutron in the nucleus into a proton, generally followed by the emission of an electron and a neutrino. The reverse can also take place for nuclei lacking in neutrons (i.e., the proton in the nucleus is transformed into a neutron followed by the emission of a positron and a neutrino) (Id., pp. 18-19). In beta-decay, . . .
Gamma decay
Gamma decay is the transition of a nucleus from one excited state to a lower excited state with the accompanying emission of a photon. The emitted photons have energies equal to the difference between the energies of the initial and final states, and are called gamma rays (Id., p. 18). Gamma decay . . .
The fundamental law describing radioactive decay states that the probability that a nucleus will decay in a given time interval is a constant independent of time. This constant is known as the radioactive decay constant, λ , and can be related to the number of original nuclei, N, left at time t through the following expression (Id., p. 23)
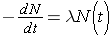
Note that λ has units of inverse time. Now, if initially N0 nuclei are present we can calculate the number of nuclei present at any later time t through the expression
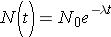
The rate at which nuclei are [_____] is given by the formula (Duderstadt & Hamilton 1976, p. 13)
Rate = 
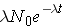
A related quantity is the radioactive half-life, T1/2, which is the length of time necessary for half of the original number of nuclei present to [_____}. The half-life can be calculated by noting
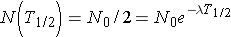
or (Id., equation 2.26)
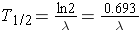
Another important quantity is that of the activity describing, or characterizing, a sample of radioactive material. The activity is the total number of disintegrations occurring per second λN(t) and is usually measured in units of curies (Ci) (Id., p.23). To derive an expression for the activity of a nuclide, we must first consider that most radioactive decay processes are a little bit more complicated than previously described. This is due to that the decaying nuclide may itself be produced by some source, R(t). The change in the number of original nuclide at a given time (or time interval) can then be expressed as
Time rate of change of the nuclide =
the rate of [_____] - the rate of [_____]loss
or symbolically
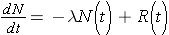
Integrating this equation and multiplying through by l gives the activity of the nuclide (Id., equation 2.30)
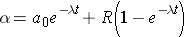
Another scenario that is often considered is the radioactive decay chain. Consider the decay chain
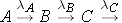
The number of nuclides of each type present can then be found through the expressions
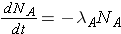
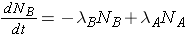
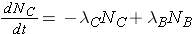
The integrated results of these equations are shown on p. 26 of the Lamarsh & Baratta. (equations 2.32 & 2.33).
As nuclear processes occur, the nuclides change in accordance with the illustration below (Chart of the Nuclides):
This content requires Flash Player 10 or higher. 
Instructions: Click each nuclide and drag it to its proper position on the chart above.
where . . .
