STABLE NUCLIDES & BINDING ENERGY
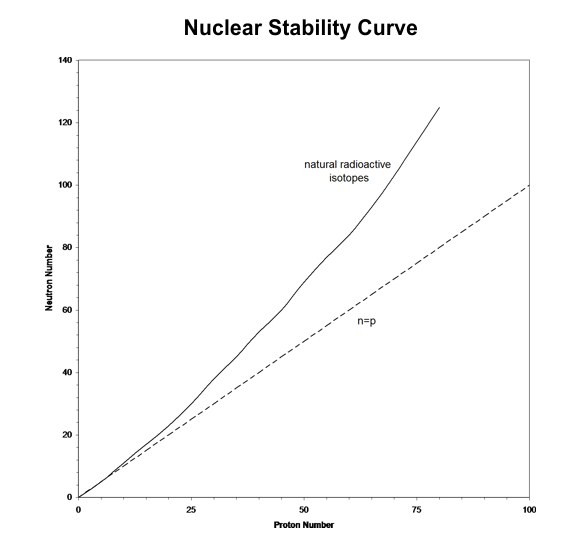
Nuclear forces acting among nucleons (neutrons & protons) in a stable nucleus are such that the ratio of A to Z increases with Z. This means that stable nuclides become [_____] neutron-rich with [_____] Z. This is illustrated below in the nuclear stability curve (Stacey 2001, Figure 1.1).
Because the actual mass of an atomic nucleus is not the sum, the stable nuclides have a mass defect. The mass defect is defined as (Id., equation 2.43)
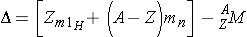
where,
∆, when expressed in energy units, is equal to the energy that it takes to break the nucleus into its constituent nucleons.
Summary
Binding energy of the nucleus = The amount of [_____] supplied energy that would be converted to mass in disassembling a nucleus into its separate nucleons.
The splitting of very high A nuclides to form intermediate-A nuclides with a higher binding energy per A value is the basis of the [_____] process for the release of nuclear energy, while the combination of low A nuclides to form higher A nuclides with a higher binding energy per A value is the basis of the [_____] process (Stacey 2001, pp. 3-4). The binding energy per nucleon as a function of Z is illustrated in Figure 2.8 of Lamarsh & Baratta.
The binding energy is also known as the [_____] energy. The separation energy, ES, of the last neutron (this is the least bound) can be calculated from the expression (Id., equation 2.45)
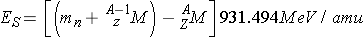
The separation energy is enough to [_____] a neutron [_____] the nucleus but it does not provide any kinetic energy to the nucleus.
It should also be mentioned that there are some "magic" nuclei with nucleons know as "magic numbers". The "magic numbers" (neutrons or protons) are: hint - consult the periodic table.
As an example, 
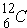is a weak absorber because of "magic number". Further, 
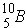is a strong absorber because it has 1 less neutron than the "magic number". Also, when there are an odd number of neutrons, the last neutron is weakly bound.
